~home ~info ~blog ~code ~links ~mindwalled

Primer to Numbers and Endianness in Computing

I’ve been working on my C fluency as of late but taking on a handful of random projects to tackle for when I have time. For one of these projects, I decided to write a chip-8 emulator. I’ll spare you the details of the actual implementation for now and instead touch on a rather interesting topic on the forefront of my mind as I have been working on this emulator: number systems and endianness. While the latter isnt really all that important for this project, I think both are a interesting in their own right and I wanted to write a summary on both.

Number Systems in Computing

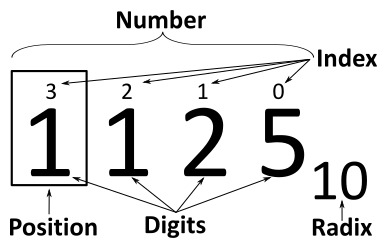
For most of history, humans have been using a positional number system to represent values. Commonly, we have used a base-10 system to represent our numbers, meaning that 10 becomes the radix, or the place value, for numbers.

Positional notation of the Base-10 number system

Computers at the lowest level really have no way of representing numbers in base-10, rather since most CPUs are based of digital logic processing ‘on’ and ‘off’ signals, binary, or base 2, has become the key system for representing numbers. We can abstract “on” and “off” to 1 and 0 respectively in binary. This is the basis of how numbers are represented on computer hardware. In the image above, our radix is now 2 instead of 10 and we do place value in the exact same way, but we add a new place value every time we reach a multiple of 2.

binary:  11 ( [2^1 * 1] + [2^0 * 1] )
decimal:  3 ( [10^0 * 3] )
The two numbers above are eqivalent representations of the number '3' in decimal

Now this number system is pretty great, but if you do anything low-level with computing, you will see this rarely, instead, most programmers use another number system to represent binary data that has a lot of unique benefits compared to raw binary. This system is hexadecimal, or base-16. Numbers start from zero and go to F (or 15), place moves over once we hit F0, or 16. This system has a rather large amount of benefit when dealing with manipulating binary data, particularly when bit widths are considered.

A byte is a binary number consists of eight bits (or places). Thus the number 11111111 or 255 in decimal is a single byte of data, half of this number, 1111 or 15 is called a nibble. What makes hex so useful is that it is a multiple of 2, 4, and 8, thus we can represent a byte as 0xFF, and a nibble as 0xF (0x is a common prefix for hex numbers). Thus a hex number with 2(n) digits is n bytes long. It also abstracts the over-verbosity of binary into a format that is both easier to work with and easier to read¹.

bcal> c 0xF
 (b) 1111
 (d) 15
 (h) 0xf
bcal> c 0xFF
 (b) 11111111
 (d) 255
 (h) 0xff

Endianness

Endianness is the property of how multi-byte (remember: multi-byte) values are stored in memory. Chip8 containes 35 opcodes that are all represented as big-endian multi-byte values. So what actually is the magic property “endianness”? Consider a normal base-10 number 512. We read this number as a some of 10^n powers:

(10^2 * 5) + (10^1 * 1) + (10^0 * 2)

Thus 512 is “broken up” into 3 place parts: 500, 10, and 2. We represent the number ‘512’ buy taking 500 as the most ‘significant’ digit, or the digit with the most weight, and sticking it on the leftmost side of the number. Then we build on with the remaining digits in descending ‘significance’ based on place value. So endianness is basically how we represent sequences of multi-byte values in aa similar manner, thus if we have the number 0xAABB as our multi-byte value, we can represent it in two ways based on endinannes:

Given Hex: 0xAABB

In memory:
    Big endian:    | AA | BB | or (16^1 * AA), (16^0 * BB)
    Little endian: | BB | AA | or (16^0 * BB), (16^1 * AA)

Big endianness is when the most significant byte is stored first, Little endianness is when the least significant byte is stored first. I am not entirely sure the reason for using one over the other, thats research for another day, but it does play a role in some systems. However you must be careful, this is not the method of how arbitrary data is stored. For instance lets say I have a char[4] = { 'J', 'o', 'h', 'n' }; in memory, it would NOT be represented as 'n' | 'h' | 'o' | 'J' in memory. Each char is a single 8 bit value, or one byte. Instead if we had an array of multi-bit values, they would appear as the following in memory:

// in hex: { 0xFA12, 0xCE34 };
int a[4] = { 64018, 52803 };

// In memory:
//      Big endian:    [ 0xFA | 0x12 ], [ 0xCE | 0x34 ]
//      Little endian: [ 0x12 | 0xFA ], [ 0x34 | 0xCE ]

In most systems you don’t notice the difference, because the hardware will convert from little endian to what you expect. Thus given the above example, if you were to inspect the first 2 bytes of the 1st element of array a, you would get 0xFA12 on both a little and big endian system. However if you were only inspecting a single byte of the first element of a, you would get 0xFA on a big endian system and 0x12 on a little endian system. The actual width of the int depends on multiple factors, but the overall message of the pseudocode is the same.

Overall I find these minute nuances of computers quite interesting, even if I rarely deal with them much day to day.

<= Previous Next =>